G02 Engl
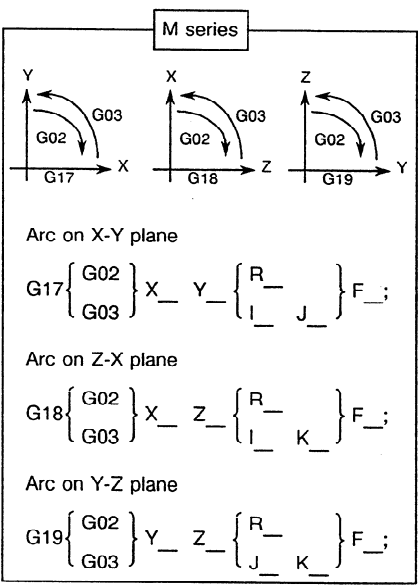
G02: clockwise circular interpolation
G03: counterclockwise circular interpolation
G17: Interpolation level XY
G18: Interpolation level ZX
G19: Interpolation level YZ
Syntax:
G17 | G18 | G19
The choice of interpolation plane determines in which plane the arc is machined. At the same time, it determines which two coordinate axes out of three (XYZ) determine the end point of the arc. The third coordinate results in a helix, if given.
G02 (G03) X_ Y_ Z_ {I_ J_ K_} | {R_} | F_
X_ Y_ Z_: Coordinates of the end point of the arc (in the interpolation plane).
I_ J_ K_: Distance of the center of the arc from the starting point (in the interpolation plane - only 2 out of three are given). The distance is given relative to the starting point.
R_: Alternatively, the radius of the circle (in which case no arguments to IJK are given).
Circular interpolation is intended for milling curved shapes and takes place at the current feed rate. The G-code representation allows the arc to be interpolated only in the planes defined by the three basic axes of the machine. In an arbitrary plane, a circle cannot be interpolated. The level is selected before the function with codes G17 .. G19 and they are modal to each other.
The arc is defined by the endpoints and the center of the circle. The center point should be the same distance from both endpoints or the controller will stop in error.
The starting point of the circle is the point where the tool is when the function starts. The end point is defined by XYZ coordinates (taking into account the current interpolation level).
There are two options for determining the center of a circle, either the auxiliary coordinates I, J, K, or the radius R. The auxiliary coordinates are relative such that the distance of the center from the origin is X + I, Y + J, Z + K (2 out of three considering the interpolation plane).
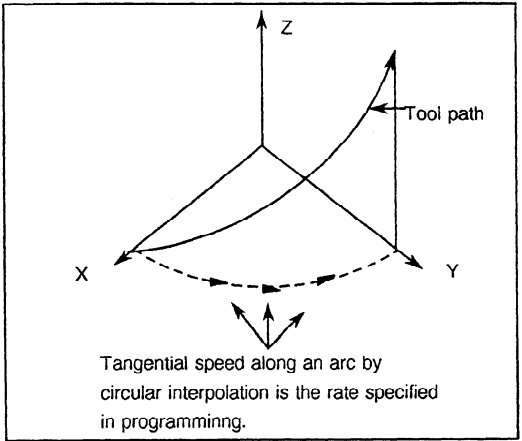
The interpolation instruction allows all three coordinates in the endpoint definition. In this case, the arc of the circle is interpolated in the selected plane, and a linear movement takes place in the direction of the third axis from the initial position to the given final coordinate. In this way, helixes, i.e. helical cylindrical dips, can be machined.
The Lota Fanuc controller works in such a way that if no endpoint is given at all, the function interpolates a full circle around the given centerpoint. This makes it particularly easy to machine circles and helical circular dips by giving a third coordinate in the normal direction of the interpolation plane from the end point.